CV

Weiwei Jin received his BS from the Department of Theoretical and Applied Mechanics, Peking University in 2012, and is currently a Ph.D. student in the Department of Mechanical Engineering of Peking University. His research area is focused on the jamming of granular materials and dense packings.
1. Computational material research with a focus on jammed packings of non-spherical particles and cluster assembly and mechanical properties of granular materials.
2. Computer simulations to study the dense crystal structure and the phase behavior of colloids and nanoparticles.

attachment: 

PDF icon CV_Weiwei Jin

RESEARCH

SOFT MATTER RESEARCH

Packings of particles have widely been used as models for condensed matter systems, such as simple liquids, glasses, crystals, and granular media.

1. Dense packings:

The square-triangle crystal of self-dual ellipsoids

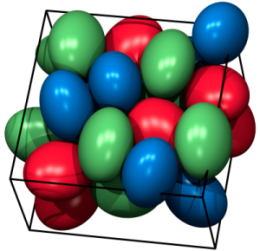
Dense crystal structures and the phase behavior of colloids and nanoparticles. 

solid-solid_transition_from_sm2_to_sq-tr_phase.mp4

A very interesting class of problems concerns the search for best possible ways to pack objects, where from the physics point of view such problems are closely related to the structures and properties of crystalline phases. For example, the densest possible packings of identical spheres include two well-known examples of crystal structures, namely the FCC and the HCP crystals. While there have been many studies on the densest possible packings of spheres in different contexts, problems concerning the densest possible packings of non-spherical particles remain largely unexplored. 

2. Granular materials:

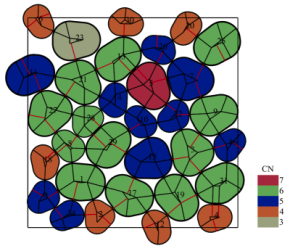
Jammed packings of non-spherical particles, cluster assembly, mechanical properties and shear response.

simple_shear_of_circulo-triangles.mp4

On the other hand, the jamming transition, at which a system undergoes transition from a fluid-like to a solid-like state but remains disordered, has received particular attention from the scientific community, where in the vicinity of this critical point a variety of structural and mechanical quantities exhibit power-law scaling with respect to distances from the critical point.