In ultrafast experiments, an optical pump pulse often generates transient domain walls of the order parameter in materials with spontaneous symmetry breaking. Whether the domain wall decays, and if so, how it decays, remains a puzzle. We clarify the decaying process of such a domain wall that is caused by fluctuations of the order parameters. The decay process comprises two non-trivial stages. During the first stage, exponentially growing thermal fluctuations convert the domain wall into an interface with randomly distributed topological defects. In the second stage, the topological defects undergo a coarsening dynamics within the interface.

Methods: Time-dependent Ginzburg Landau equation, Vortex dynamics, Analytic calculation + numerics.
2. Antiparticle of exciton in semimetals. LK, R Shindou, and Y Zhang, PhysRevB.106.235145
We propose an antiparticle analog of the exciton (antiexciton) in semimetals as an emergent collective excitation. By solving the Bethe-Salperer equation for inter-band excitations and analyzing the corresponding effective field theory, we show that the inter-band collective excitations in doped semimetals are generally comprised of both excitons and antiexcitons carrying opposite U(1) charge.

Methods: Many-body perturbation theory, Bethe-Salpeter equation, Klein-Gordon theory.
3. Dynamical Regime of Layer-Pseudospin Ferromagnetism in Biased Bilayers. LK, R Shindou, and Z Sun, in preparation.
The bilayer quantum Hall system is a promising platform to realize a correlated state, the layer-pseudospin ferromagnetism. We show that the correlated state could be driven into the NESS by the voltage control. Physical consequences are discussed.
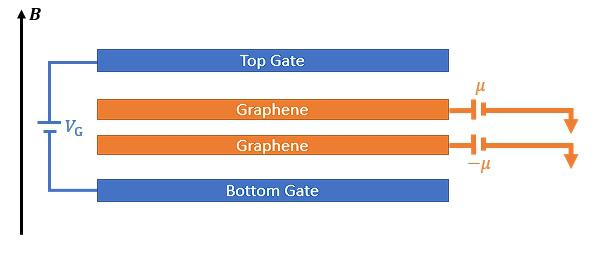
Methods: Non-equilibrium field theory.
4. Symmetry-dependent antiferromagnetic proximity effects on valley splitting. Chengyang Xu, LK, and Weidong Luo, PhysRevB.107.125408
A ferromagnetic proximity that breaks the time-reversal symmetry (TRS) is often used to lift the valley degeneracy of the transition-metal dichalcogenides (TMDc). Whether the antiferromagnetic (AFM) proximity, which also breaks the TRS but provides zero net magnetization, lifts the valley degeneracy remains an interesting question. We show that the valley degeneracy is protected if an “effective” TRS such as a “time-reversal + fractional translation” symmetry exists. Combining symmetry analysis, a tight-binding model, and a density-function-theory calculation, we study valley degeneracy/splitting in TMDc for various configurations of the AFM proximity.
![]() . I was born in 1998 in Shandong province.
. I was born in 1998 in Shandong province. 


